Коэффициент корреляции пирсона: онлайн калькулятор

Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel

КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.

Примеры использования функции КОРРЕЛ в Excel

Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:

24

Алгоритм расчёта выглядит следующим образом:

25

Отображенный показатель близок к 1. Результат:

26

Определение коэффициента корреляции влияния действий на результат

Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.

27

Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:

• =КОРРЕЛ(А3:А17;В3:В17).
• =КОРРЕЛ(А3:А17;С3:С17).

Результаты:

28

Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.

Анализ популярности контента по корреляции просмотров и репостов видео

Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:

29

Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:

0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная  прямая зависимость»;»Сильная обратная зависимость»);»Слабая зависимость или ее отсутствие»)’ class=’formula’>

Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:

30

Теперь производим построение графика:

31

Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:

32

Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’ class=’formula’>. Получаем следующие результаты:

33

Особенности использования функции КОРРЕЛ в Excel

Данная функция имеет нижеприведенные особенности:

1. Не учитываются ячейки пустого типа.
2. Не учитываются ячейки, в которых находится информация типа Boolean и Text.
3. Двойное отрицание «—» применяется для учёта логических величин в виде чисел.
4. Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.

Анализ полученных результатов

После корректного заполнения всех параметров и нажатия кнопки OK отобразятся результаты анализа (в зависимости от выбранного способа). В нашем случае – на отдельном листе.

Ключевым показателем здесь является R-квадрат (коэффициент детерминации), значение которого характеризует качество модели. Приемлемым считается значение не менее 0,5 (или 50%).

Также следует обратить внимание на ячейку, расположенную на пересечении строки “Y-пересечение” и столбца “Коэффициенты”. Здесь показывается, каким будет значение Y (количество осадков), если все остальные факторы будут равны нулю

Ячейка на пересечении строки “Переменная X 1” и столбца “Коэффициенты” содержит значение, характеризующее степень зависимости Y от X. Коэф. 0,89 в нашем случае говорит о достаточно сильной связи между переменными.

3) уравнение линейной регрессии на

Это и есть та самая оптимальная прямая , которая проходит максимально близко ко всем точкам. Обычно её находят методом наименьших квадратов, и мы пойдём знакомым путём

Заполним расчётную таблицу:
Обратите внимание, что в отличие от задач урока МНК у нас появился дополнительный столбец , он потребуется в дальнейшем, для расчёта коэффициента корреляции

Сократим оба уравнения на 2, всё попроще будет:

Систему решим по формулам Крамера: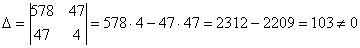, значит, система имеет единственное решение.

Таким образом, искомое уравнение регрессии: 

Данное уравнение показывает, что с увеличением количества прогулов («икс») на 1 единицу суммарная успеваемость падает в среднем на 6,0485 – примерно на 6 баллов. Об этом нам рассказал коэффициент «а»

И обратите особое внимание, что эта функция возвращает нам средние (среднеожидаемые) значения «игрек» для различных значений «икс»

Почему это регрессия именно « на » и о происхождении самого термина «регрессия» я рассказал чуть ранее, в параграфе . Если кратко, то полученные с помощью уравнения средние значения успеваемости («игреки») регрессивно возвращают нас к первопричине – количеству прогулов. Вообще, регрессия – не слишком позитивное слово, но какое уж есть.

Найдём пару удобных точек для построения прямой: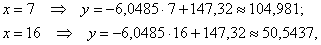
отметим их на чертеже (малиновый цвет) и проведём линию регрессии: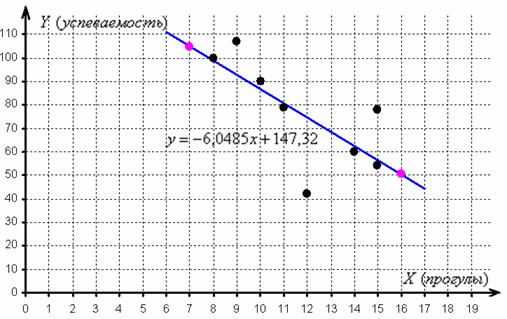

Говорят, что уравнение регрессии аппроксимирует (приближает) эмпирические данные (точки), и с помощью него можно интерполировать (восстановить) неизвестные промежуточные значения, так при количестве прогулов  среднеожидаемая успеваемость составит  балла.

И, конечно, осуществимо прогнозирование, так при  среднеожидаемая успеваемость составит  баллов. Единственное, нежелательно брать «иксы», которые расположены слишком далеко от эмпирических точек, поскольку прогноз, скорее всего, не будет соответствовать действительности. Например, при  значение  может вообще оказаться невозможным, ибо у успеваемости есть свой фиксированный «потолок». И, разумеется, «икс» или «игрек» в нашей задаче не могут быть отрицательными.

Второй вопрос касается тесноты зависимости. Очевидно, что чем ближе эмпирические точки к прямой, тем теснее линейная корреляционная зависимость – тем уравнение регрессии достовернее отражает ситуацию, и тем качественнее полученная модель. И наоборот, если многие точки разбросаны вдали от прямой, то признак  зависит от  вовсе не линейно (если вообще зависит) и линейная функция плохо отражает реальную картину.

Прояснить данный вопрос нам поможет:

Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки

В сегодняшней статье речь пойдет о том, как переменные могут быть связаны друг с другом. С помощью корреляции мы сможем определить, существует ли связь между первой и второй переменной. Надеюсь, это занятие покажется вам не менее увлекательным, чем предыдущие!

Корреляция измеряет мощность и направление связи между x и y. На рисунке представлены различные типы корреляции в виде графиков рассеяния упорядоченных пар (x, y). По традиции переменная х размещается на горизонтальной оси, а y — на вертикальной.

График А являет собой пример положительной линейной корреляции: при увеличении х также увеличивается у, причем линейно. График В показывает нам пример отрицательной линейной корреляции, на котором при увеличении х у линейно уменьшается. На графике С мы видим отсутствие корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.

Наконец, график D — это пример нелинейных отношений между переменными. По мере увеличения х у сначала уменьшается, потом меняет направление и увеличивается.

Оставшаяся часть статьи посвящена линейным взаимосвязям между зависимой и независимой переменными.

Коэффициент корреляции

Коэффициент корреляции, r, предоставляет нам как силу, так и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между — 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной (график A на рисунке), а когда значение r отрицательно, связь также отрицательна (график В). Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует график С).

Сила связи между х и у определяется близостью коэффициента корреляции к — 1.0 или +- 1.0. Изучите следующий рисунок.

График A показывает идеальную положительную корреляцию между х и у при r = + 1.0. График В — идеальная отрицательная корреляция между х и у при r = — 1.0. Графики С и D — примеры более слабых связей между зависимой и независимой переменными.

Коэффициент корреляции, r, определяет, как силу, так и направление связи между зависимой и независимой переменными. Значения r находятся в диапазоне от — 1.0 (сильная отрицательная связь) до + 1.0 (сильная положительная связь). При r= 0 между переменными х и у нет никакой связи.

Мы можем вычислить фактический коэффициент корреляции с помощью следующего уравнения:

Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение непонятных символов, но прежде чем ударяться в панику, давайте применим к нему пример с экзаменационной оценкой. Допустим, я хочу определить, существует ли связь между количеством часов, посвященных студентом изучению статистики, и финальной экзаменационной оценкой. Таблица, представленная ниже, поможет нам разбить это уравнение на несколько несложных вычислений и сделать их более управляемыми.

Как видите, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция. Преподаватели будут весьма рады узнать об этом.

Какова выгода устанавливать связь между подобными переменными? Отличный вопрос. Если обнаруживается, что связь существует, мы можем предугадать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем точнее будет наше предсказание.

Использование Excel для вычисления коэффициентов корреляции

Я уверен, что, взглянув на эти ужасные вычисления коэффициентов корреляции, вы испытаете истинную радость, узнав, что программа Excel может выполнить за вас всю эту работу с помощью функции КОРРЕЛ со следующими характеристиками:

КОРРЕЛ (массив 1; массив 2),

массив 1 = диапазон данных для первой переменной,

массив 2 = диапазон данных для второй переменной.

Например, на рисунке показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.

Ковариация

Пусть математическое ожидание и дисперсия случайной величины X равны, соответственно, μ_x и σ_x2. А математическое ожидание и дисперсия
случайной величины Y равны, соответственно, μ_y и σ_y2.

Для независимых случайных величин X и Y всегда матожидание произведения случайных величин равно произведению их матожиданий по отдельности:

M(xy) = μ_xμ_y

А для зависимых случайных величин это равенство не выполняется.

Ковариация, это отклонение математического ожидания произведения двух случайных величин от произведения их математических ожиданий:

cov(x,y) ≡ σ_xy = σ_yx = M(xy) — μ_xμ_y = M[(x-μ_x)(y-μ_y)]

Ковариация характеризует отклонение матожидания произведения двух случайных величин от произведения матожиданий этих величин. Так как это отклонение бывает только для зависимых величин, то ковариация
характеризует степень этой зависимости. Чем она больше отличается от нуля, тем больше зависимость.

Матрица ковариаций для нескольких случайных величин X, Y, …, Z всегда симметрична, причем на главной диагонали этой матрицы всегда стоят положительные числа, равные дисперсиям
случайных величин X, Y, …, Z.

Корреляционный анализ в Excel

Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.

Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.

Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.

Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.

Для нахождения парных коэффициентов применяется функция КОРРЕЛ.

Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.

Ставим курсор в любую ячейку и нажимаем кнопку fx.

1. В категории «Статистические» выбираем функцию КОРРЕЛ.
2. Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
3. Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.

Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).

Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.

Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:

Значения коэффициента корреляции

Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока, в которой определенному числовому значению соответствует качественная характеристика.

• 0-0,3 – корреляционная связь очень слабая;
• 0,3-0,5 – слабая;
• 0,5-0,7 – средней силы;
• 0,7-0,9 – высокая;
• 0,9-1 – очень высокая сила корреляции.

Шкала может использоваться и для отрицательной корреляции. В этом случае качественные характеристики заменяются на противоположные.

Можно воспользоваться упрощенной шкалой Челдока, в которой выделяется всего 3 градации силы корреляционной связи:

• очень сильная – показатели ±0,7 — ±1;
• средняя – показатели ±0,3 — ±0,699;
• очень слабая – показатели 0 — ±0,299.

Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.

История разработки критерия корреляции

Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.

Для чего используется критерий корреляции Пирсона?

Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.

Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.

Условия и ограничения применения критерия хи-квадрат Пирсона

1. Сопоставляемые показатели должны быть измерены в количественной шкале (например, частота сердечных сокращений, температура тела, содержание лейкоцитов в 1 мл крови, систолическое артериальное давление).
2. Посредством критерия корреляции Пирсона можно определить лишь наличие и силу линейной взаимосвязи между величинами. Прочие характеристики связи, в том числе направление (прямая или обратная), характер изменений (прямолинейный или криволинейный), а также наличие зависимости одной переменной от другой – определяются при помощи регрессионного анализа.
3. Количество сопоставляемых величин должно быть равно двум. В случае анализ взаимосвязи трех и более параметров следует воспользоваться методом факторного анализа.
4. Критерий корреляции Пирсона является параметрическим, в связи с чем условием его применения служит нормальное распределение каждой из сопоставляемых переменных. В случае необходимости корреляционного анализа показателей, распределение которых отличается от нормального, в том числе измеренных в порядковой шкале, следует использовать коэффициент ранговой корреляции Спирмена.
5. Следует четко различать понятия зависимости и корреляции. Зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.

Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.

В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.

Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов

1) Эмпирический коэффициент детерминации:

 – есть отношение межгрупповой дисперсии к общей дисперсии.

Общая дисперсия  учитывает ВСЕ причины, которые влияют на вариацию признака-результата (прибыли). Межгрупповая дисперсия  учитывает влияние фактора, положенного в основу группировки (выпуска продукции).

Эмпирический коэффициент детерминации характеризует ДОЛЮ влияния группировочного фактора (выпуска продукции). Данный коэффициент изменяется в пределах , и чем он ближе к единице, тем сильнее влияние группировочного фактора на признак-результат (прибыль).

Дело за малым – вычислить  и .

В «шапке» и в левом столбце комбинационной таблицы (см. выше) у нас находятся два интервальных вариационных ряда и сначала нужно перейти к дискретным рядам, выбрав в качестве вариант  и  середины соответствующих интервалов: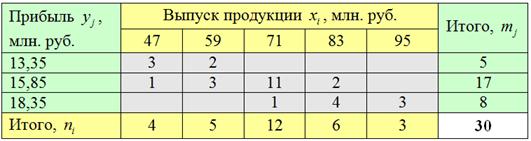

На всякий случай примеры расчёта: .

Вычислим общую среднюю признака-результата: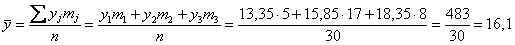 млн. руб.

и общую дисперсию: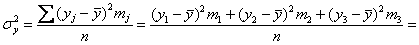

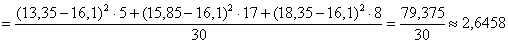
Разбираемся с межгрупповой дисперсией. Для её нахождения вычислим групповые или, как их называют, условные средние. При условии  средняя прибыль составит: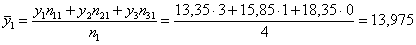 млн. руб.
и давайте ещё в качестве закрепляющего примера приведу расчёт для :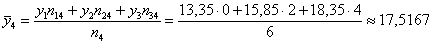 млн. руб.

Промежуточные вычисления удобно заносить рядышком, наращивая комбинационную таблицу: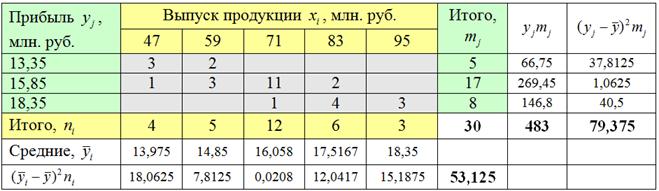

Полагаю, после моих видео вам не составит труда автоматизировать эти вычисления в Экселе. Вычислим межгрупповую дисперсию: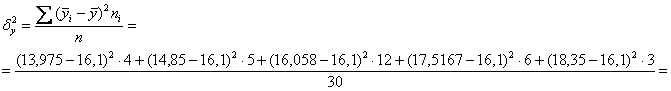

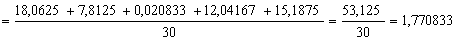
В качестве факультативного задания предлагаю самостоятельно вычислить групповые дисперсии ( по каждой из пяти групп), внутригрупповую дисперсию и проверить правило сложения дисперсий . Я выполнил это в обязательном порядке, дабы избежать ошибок.

Вычислим эмпирический коэффициент детерминации: – таким образом, 66,93% вариации прибыли обусловлено изменением  выпуска продукции. Остальные 33,07% вариации обусловлены другими факторами.

Исходя из правило сложения дисперсий , легко понять, что за остальную вариацию отвечает внутригрупповая дисперсия , графически она характеризует меру разброса частот в серых столбцах (см. таблицу выше).

Теперь повторим суть коэффициента детерминации. Чем ближе  к единице, тем больше межгрупповая дисперсия  и меньше . Высокое значение  говорит о том, что групповые средние  знАчимо отличаются от общей средней , то есть изменение значений «икс» приводит к существенному изменению значений «игрек». Иными словами, признак-фактор действительно оказывает сильное влияние. При этом внутригрупповая  дисперсия  будет малА и частоты в серой области примут выраженный диагональный вид. В предельном случае   (и нулевом значении ) речь идёт о строгой функциональной зависимости.

Обратно, малые значения  обусловлены тем, что межгрупповая дисперсия  близкА к нулю – по той причине, что групповые средние  близкИ к общей средней . Это означает, что на изменение значений «икс» – «игреки» «откликаются» слабо. При этом внутригрупповая дисперсия  будет большой – это значит, что дисперсия в группах существенна и частоты в серых столбцах более разбросаны – фактически они заполнят всю серую область и, естественно, утратят диагональный вид.

Кто всё понял, тот монстр 🙂

Следующий показатель:

Расчет коэффициента корреляции

Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

1. Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.

В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».

Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.

В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

Жмем на кнопку «OK».

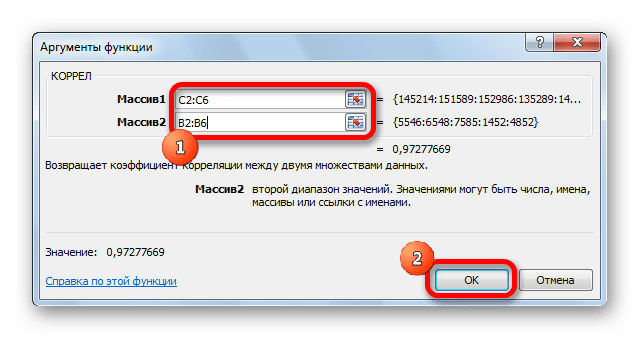
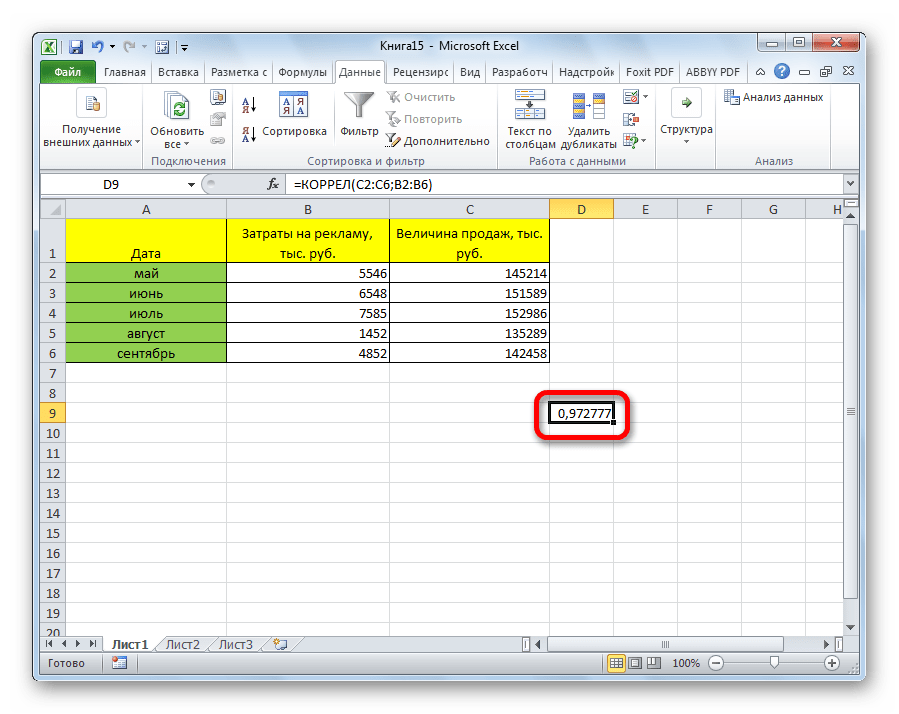
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

1. Переходим во вкладку «Файл».

В открывшемся окне перемещаемся в раздел «Параметры».

Далее переходим в пункт «Надстройки».

В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

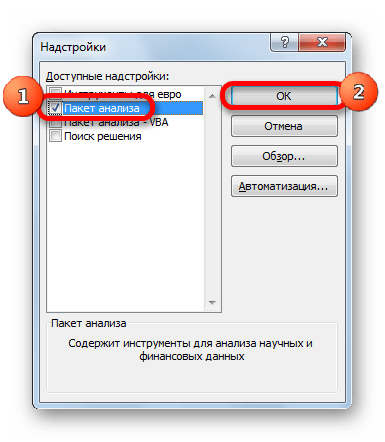
После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

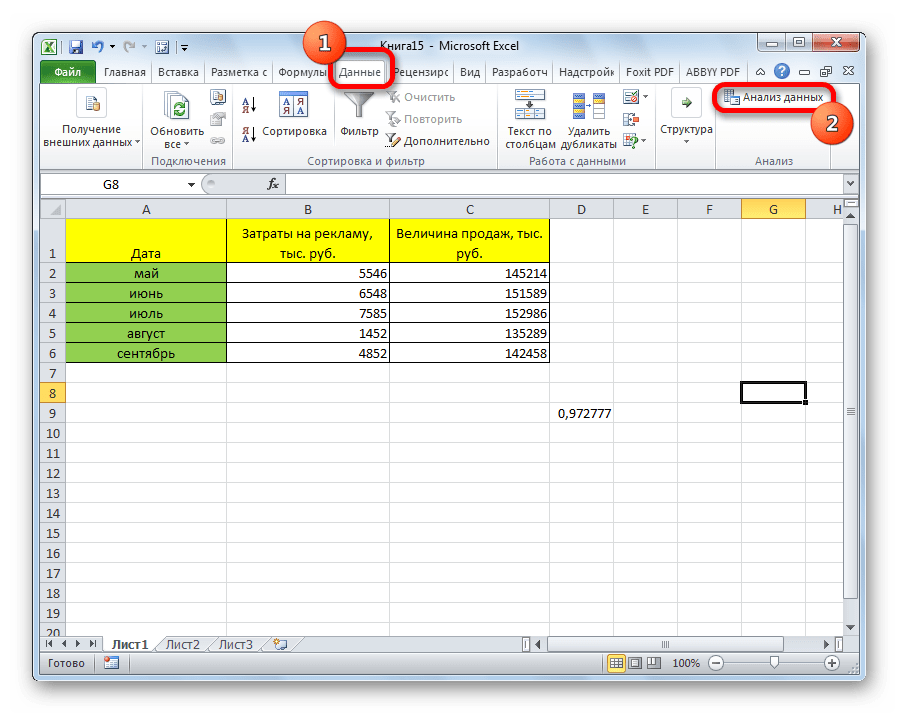
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

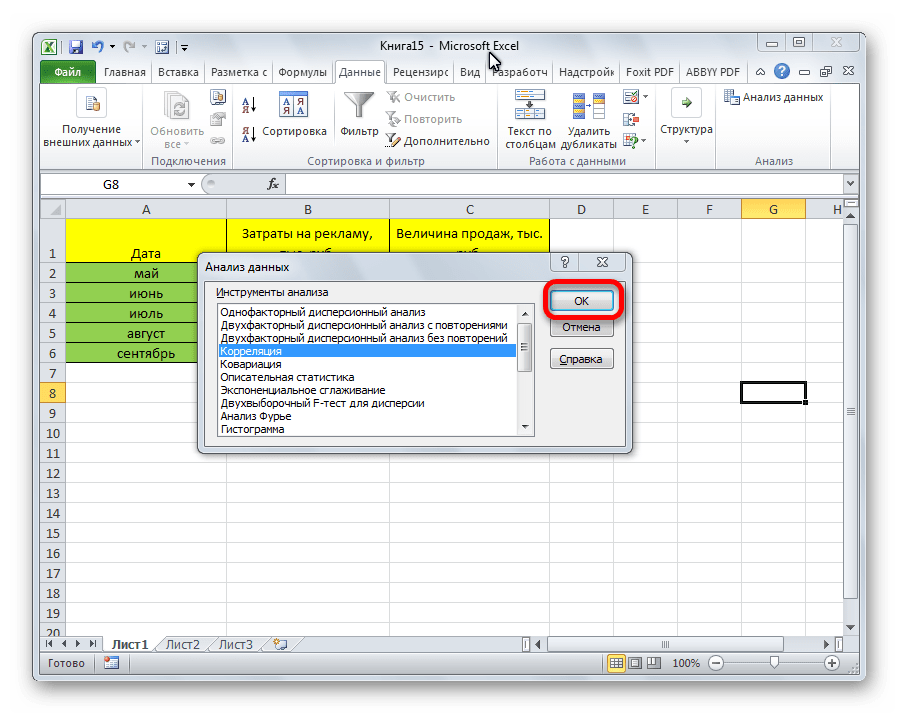
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».

Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

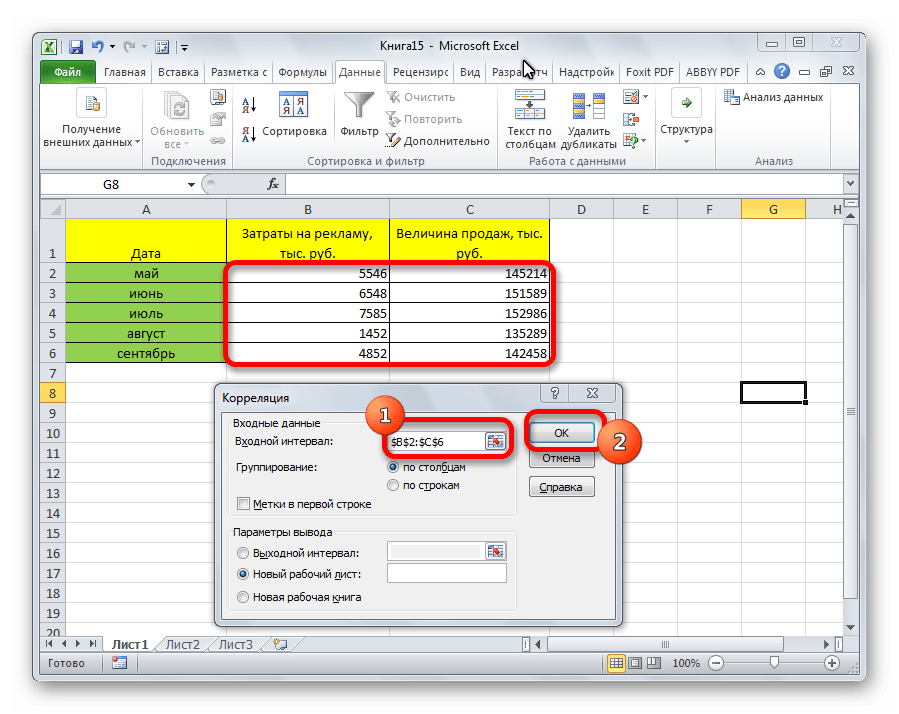
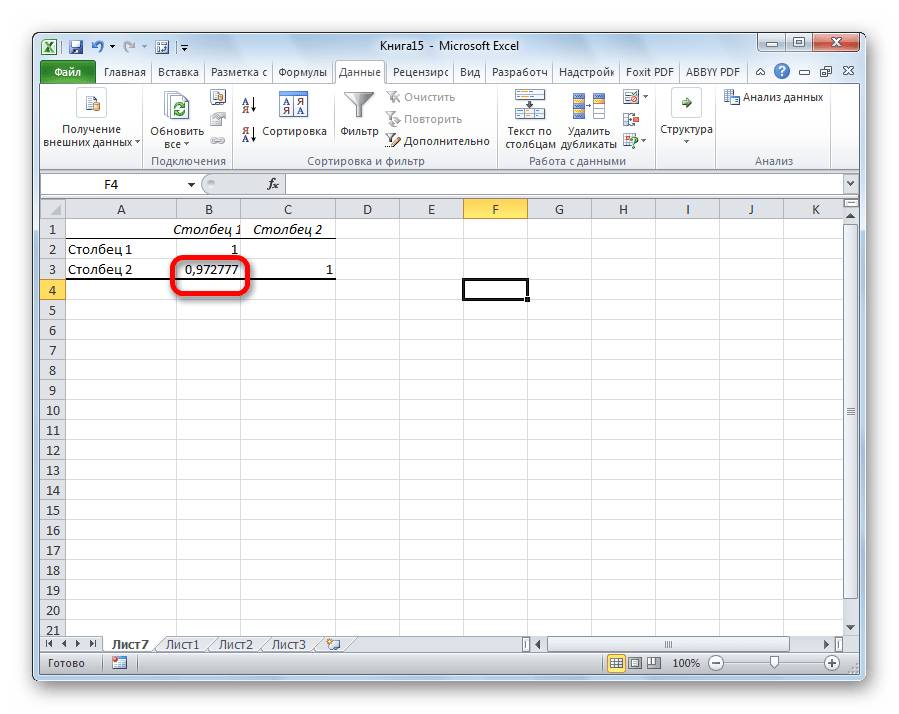
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Коэффициент корреляции и ПАММ-счета

С расчётом корреляции я как студент экономического ВУЗа познакомился еще на втором курсе

Тем не менее, долгое время недооценивал важность расчёта корреляции именно для подбора ПАММ-портфеля. 2018 год очень четко показал, что ПАММ-счета с похожими стратегиями в случае кризиса могут вести себя очень похоже

Случилось так, что с середины года отказала не просто одна стратегия управляющего, а большинство торговых систем, завязанных на активные движения валютной пары EUR/USD:

Рынок был для каждого управляющего по-своему неблагоприятным, но присутствие их всех в портфеле привело к большой просадке. Совпадение? Не совсем, ведь это были ПАММ-счета с похожими элементами в торговых стратегиях. Без опыта торговли на рынке Форекс может быть сложно понять, как это работает, но по корреляционной таблице степень взаимосвязи видна и так:

Мы ранее рассматривали корреляцию вплоть до +1, но как видите на практике даже совпадение в районе 20-30% уже говорит о некоторой схожести ПАММ-счетов и, как следствие, результатов торговли.

Чтобы снизить шансы на повторение ситуации, как в 2018 году, я считаю в портфель стоит подбирать ПАММ-счета с низкой взаимной корреляцией. По сути, нам нужны уникальные стратегии с разными подходами и разными валютными парами для торговли. На практике, конечно, сложнее подобрать прибыльные счета с уникальными стратегиями, но если хорошо покопаться в рейтинге ПАММ-счетов, то все возможно. К тому же, низкая взаимная корреляция снижает требования для диверсификации, 5-6 счетов вполне хватит.

Пару слов о расчёте коэффициента корреляции для ПАММ-счетов. Достать сами данные относительно несложно, в Альпари прямо с сайта, для остальных площадок через сайт investflow.ru. Однако с ними нужно сделать небольшие преобразования.

Данные о прибыльности ПАММов изначально хранятся в формате накопленной доходности, нам это не подходит. Корреляция стандартных графиков доходности двух прибыльных ПАММ-счетов всегда будет очень высокой, просто потому что они все движутся в правый верхний угол:

У всех счетов положительная корреляция от 0.5 и выше за редким исключением, так мы ничего не поймем. Реальное сходство стратегий ПАММ-счетов можно увидеть только по дневным доходностям. Рассчитать их не особо сложно, если знаете нужные формулы доходности. Если прибыль или убыток двух ПАММ-счетов совпадают по дням и по процентам, высока вероятность что их стратегии имеют общие элементы — и коэффициент корреляции нам это покажет:

Как видите, некоторые корреляции стали нулевыми, а некоторые остались на высоком уровне. Мы теперь видим, какие ПАММ-счета действительно похожи между собой, а какие не имеют ничего общего.

Напоследок давайте разберёмся, что делать и как посчитать корреляцию, если у вас появилась в этом необходимость.

Текст этой презентации

Расчет корреляционных зависимостей в MS Excel Подготовила учитель информатики Яценко Е.В.

Множественная корреляция в MS Excel При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять для нескольких выборок, для удобства получаемые коэф-фициенты сводят в таблицы, называемые корреляционными матрицами.

Корреляционная матрица — это квадратная таблица, в кото­рой на пересечении соответствующих строк и столбцов находятся коэффициент корреляции между соответствующими параметрами.

В MS Excel для вычисления корреляционных матриц используется процедура Корреляция из пакета Анализ данных. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

Для реализации процедуры необходимо: выполнить команду Данные — Анализ данных; 2. в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку ОК; 3. в появившемся диалоговом окне указать Входной интервал, то есть ввести ссыл­ку на ячейки, содержащие анализируемые данные. Входной интервал должен содержать не менее двух столбцов. 4. в разделе Группировка переключатель установить в соответствии с введенными данными (по столбцам или по строкам); 5. указать выходной интервал, то есть ввести ссылку на ячейку, начиная с которой будут показаны результаты анализа. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные. Нажать кнопку ОК.

В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует сам с собой

Имеются ежемесячные данные наблюдений за состоянием погоды и посещаемостью музеев и парков . Необходимо определить, существует ли взаимосвязь между состоянием погоды и посещаемостью музеев и парков. Число ясных дней Количество посетителей музея Количество посетителей парка 8 495 132 14 503 348 20 380 643 25 305 865 20 348 743 15 465 541

Решение. Для выполнения корреляционного анализа введите в диапазон A1:G3 исходные данные . Затем в меню Сервис выберите пункт Анализ данных и далее укажите строку Корреляция. В появившемся диалоговом окне укажите Входной интервал (А2:С7). Укажите, что данные рассматриваются по столбцам. Укажите выходной диапазон (Е1) и нажмите кнопку ОК.

Вывод: видно, что корреляция между состоянием погоды и посещаемостью музея равна -0,92, а между состоянием погоды и посещаемостью парка — 0,97, между посещаемостью парка и музея — 0,92. В результате анализа выявлены зависимости: сильная степень обратной линейной взаимосвязи между посещаемостью музея и количеством солнечных дней ; очень сильная прямая связь между посещаемостью парка и состоянием погоды; сильная обратная взаимосвязь между посещаемостью музея и парка .

Использование MS EXCEL для расчета корреляции

В качестве примера возьмем 2 переменные Х

иY и, соответственно,выборку состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности построим диаграмму рассеяния .

Примечание

: Подробнее о построении диаграмм см. статью Основы построения диаграмм . В файле примера для построениядиаграммы рассеяния использована диаграмма График , т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).

Расчеты корреляции

проведем для различных случаев взаимосвязи между переменными:линейной, квадратичной и приотсутствии связи .

Примечание

: В файле примера можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.

В файле примера для построения диаграммы рассеяния

в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.

Примечание

: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми

Как было сказано выше, для расчета коэффициента корреляции

в MS EXCEL существует функций КОРРЕЛ() . Также можно воспользоваться аналогичной функцией PEARSON() , которая возвращает тот же результат.

Для того, чтобы удостовериться, что вычисления корреляции

производятся функцией КОРРЕЛ() по вышеуказанным формулам, в файле примера приведено вычислениекорреляции с помощью более подробных формул:

= КОВАРИАЦИЯ.Г(B28:B88;D28:D88)/СТАНДОТКЛОН.Г(B28:B88)/СТАНДОТКЛОН.Г(D28:D88)

= КОВАРИАЦИЯ.В(B28:B88;D28:D88)/СТАНДОТКЛОН.В(B28:B88)/СТАНДОТКЛОН.В(D28:D88)

Примечание

: Квадраткоэффициента корреляции r равенкоэффициенту детерминации R2, который вычисляется при построении линии регрессии с помощью функции КВПИРСОН() . Значение R2 также можно вывести надиаграмме рассеяния , построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладкуМакет , затем в группеАнализ нажмите кнопкуЛиния тренда и выберитеЛинейное приближение ). Подробнее о построении линии тренда см., например, в статье о методе наименьших квадратов .