Как найти корреляцию в excel

Значения коэффициента корреляции

Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока, в которой определенному числовому значению соответствует качественная характеристика.

• 0-0,3 – корреляционная связь очень слабая;
• 0,3-0,5 – слабая;
• 0,5-0,7 – средней силы;
• 0,7-0,9 – высокая;
• 0,9-1 – очень высокая сила корреляции.

Шкала может использоваться и для отрицательной корреляции. В этом случае качественные характеристики заменяются на противоположные.

Можно воспользоваться упрощенной шкалой Челдока, в которой выделяется всего 3 градации силы корреляционной связи:

• очень сильная – показатели ±0,7 — ±1;
• средняя – показатели ±0,3 — ±0,699;
• очень слабая – показатели 0 — ±0,299.

Как рассчитать коэффициент корреляции в Excel

Если коэффициент равен 0, это говорит о том, что взаимосвязь между значениями отсутствует. Чтобы найти взаимосвязь между переменными и у, воспользуйтесь встроенной функцией Microsoft Excel «КОРРЕЛ». Например, для «Массив1» выделите значения у, а для «Массив2» выделите значения х. В итоге вы получите рассчитанный программой коэффициент корреляции. Далее необходимо вычислить разницу между каждым x и xср, и yср. В выбранных ячейках напишите формулы x-x, y-. Не забудьте закрепить ячейки со средними значениями. Полученный результат и будет искомым коэффициентом корреляции.

Приведенная выше формула расчета коэффициента Пирсона, показывает насколько трудоемок этот процесс если выполнять его вручную. Второе, порекомендуйте, пожалуйста, какой вид корреляционного анализа можно использовать для разных выборок с большим разбросом данных? Как мне статистически доказать достоверность отличий между группой старше 60 лет и всеми остальными?

Проверяем значимость коэффициента корреляции (проверяем гипотезу зависимости).

Поскольку оценка коэффициента корреляции вычислена на конечной выборке, и поэтому может отклоняться от своего генерального значения,
необходимо проверить значимость коэффициента корреляции. Проверка производится с помощью t
-критерия:

t =

R x,y √ n — 2 √ 1 — R 2 x,y

(2.1)

Случайная величина t

следует t
-распределению Стьюдента
и по таблице t
-распределения необходимо найти критическое значение критерия (t
кр.α) при заданном уровне
значимости α
. Если вычисленное по формуле (2.1) t
по модулю окажется меньше
чем t
кр.α , то зависимости между случайными величинами X и Y нет. В противном случае, экспериментальные
данные не противоречат гипотезе о зависимости случайных величин.

2.1.

t =

-0.72028 √ 26 — 2 √ 1 — (-0.72028) 2

= -5.08680

2.2.

Искомое значение t
кр.α располагается на пересечении строки соответствующей числу степеней свободы
и столбца соответствующего заданному уровню значимости α
. В нашем случае число степеней свободы есть n — 2 = 26 — 2 = 24
и α
= 0.05
,
что соответствует критическому значению критерия t
кр.α = 2.064
(см. табл. 2)

Таблица 2 t
-распределение

Число степеней свободы(n — 2)	α = 0.1	α = 0.05	α = 0.02	α = 0.01	α = 0.002	α = 0.001
1	6.314	12.706	31.821	63.657	318.31	636.62
2	2.920	4.303	6.965	9.925	22.327	31.598
3	2.353	3.182	4.541	5.841	10.214	12.924
4	2.132	2.776	3.747	4.604	7.173	8.610
5	2.015	2.571	3.365	4.032	5.893	6.869
6	1.943	2.447	3.143	3.707	5.208	5.959
7	1.895	2.365	2.998	3.499	4.785	5.408
8	1.860	2.306	2.896	3.355	4.501	5.041
9	1.833	2.262	2.821	3.250	4.297	4.781
10	1.812	2.228	2.764	3.169	4.144	4.587
11	1.796	2.201	2.718	3.106	4.025	4.437
12	1.782	2.179	2.681	3.055	3.930	4.318
13	1.771	2.160	2.650	3.012	3.852	4.221
14	1.761	2.145	2.624	2.977	3.787	4.140
15	1.753	2.131	2.602	2.947	3.733	4.073
16	1.746	2.120	2.583	2.921	3.686	4.015
17	1.740	2.110	2.567	2.898	3.646	3.965
18	1.734	2.101	2.552	2.878	3.610	3.922
19	1.729	2.093	2.539	2.861	3.579	3.883
20	1.725	2.086	2.528	2.845	3.552	3.850
21	1.721	2.080	2.518	2.831	3.527	3.819
22	1.717	2.074	2.508	2.819	3.505	3.792
23	1.714	2.069	2.500	2.807	3.485	3.767
24	1.711	2.064	2.492	2.797	3.467	3.745
25	1.708	2.060	2.485	2.787	3.450	3.725
26	1.706	2.056	2.479	2.779	3.435	3.707
27	1.703	2.052	2.473	2.771	3.421	3.690
28	1.701	2.048	2.467	2.763	3.408	3.674
29	1.699	2.045	2.462	2.756	3.396	3.659
30	1.697	2.042	2.457	2.750	3.385	3.646
40	1.684	2.021	2.423	2.704	3.307	3.551
60	1.671	2.000	2.390	2.660	3.232	3.460
120	1.658	1.980	2.358	2.617	3.160	3.373
∞	1.645	1.960	2.326	2.576	3.090	3.291

2.2.

Абсолютное значение t
-критерия не меньше критического t
= 5.08680,
t
кр.α = 2.064,
следовательно экспериментальные данные, с вероятностью 0.95
(1 — α
),
не противоречат гипотезе
о зависимости случайных величин X и Y.

Расчет коэффициента корреляции

Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

1. Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
2. В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
3. Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.

   В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

   Жмем на кнопку «OK».

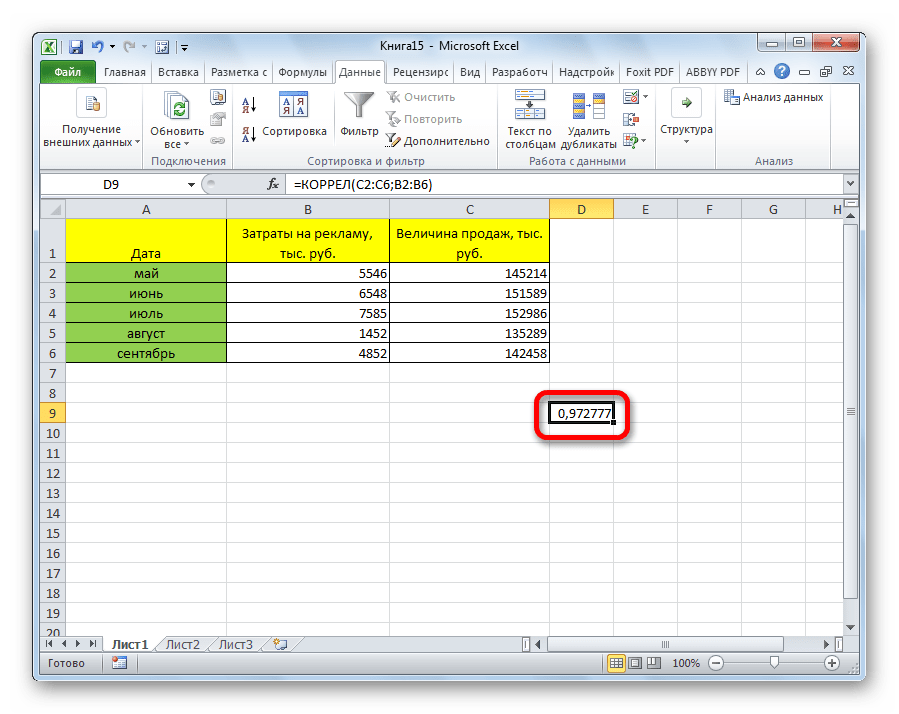
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

1. Переходим во вкладку «Файл».
2. В открывшемся окне перемещаемся в раздел «Параметры».
3. Далее переходим в пункт «Надстройки».
4. В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
5. В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
6. После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
7. Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
8. Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».

   Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

   В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

   Когда все настройки установлены, жмем на кнопку «OK».

Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Да Нет

Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.

Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.

Вычисление коэффициента посредством мастера функций

Предположим, что требуется установить связь между затратами на рекламу и объемом продаж какой-либо продукции. Для этого будем использовать коэффициент корреляции в Excel.

1. Кликнуть по ячейке, в которой должен появиться результат.
2. Нажать кнопку «Вставить формулу».
3. В появившемся окне выбрать категорию «Полный алфавитный перечень».
4. Найти и активировать функцию «КОРРЕЛ».
5. Кликнуть «ОК».
6. В открывшемся окне аргументов поставить курсор в поле «Массив 1», выделить первый столбец с данными.
7. Поставить курсор в поле «Массив 2», выделить второй столбец из таблицы.
8. Кликнуть «ОК».

В выделенной ячейке появляется результат вычислений корреляции в Excel.

Использование MS EXCEL для расчета корреляции

В качестве примера возьмем 2 переменные Х

иY и, соответственно,выборку состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности построим диаграмму рассеяния .

Примечание

: Подробнее о построении диаграмм см. статью Основы построения диаграмм . В файле примера для построениядиаграммы рассеяния использована диаграмма График , т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).

Расчеты корреляции

проведем для различных случаев взаимосвязи между переменными:линейной, квадратичной и приотсутствии связи .

Примечание

: В файле примера можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.

В файле примера для построения диаграммы рассеяния

в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.

Примечание

: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми

Как было сказано выше, для расчета коэффициента корреляции

в MS EXCEL существует функций КОРРЕЛ() . Также можно воспользоваться аналогичной функцией PEARSON() , которая возвращает тот же результат.

Для того, чтобы удостовериться, что вычисления корреляции

производятся функцией КОРРЕЛ() по вышеуказанным формулам, в файле примера приведено вычислениекорреляции с помощью более подробных формул:

= КОВАРИАЦИЯ.Г(B28:B88;D28:D88)/СТАНДОТКЛОН.Г(B28:B88)/СТАНДОТКЛОН.Г(D28:D88)

= КОВАРИАЦИЯ.В(B28:B88;D28:D88)/СТАНДОТКЛОН.В(B28:B88)/СТАНДОТКЛОН.В(D28:D88)

Примечание

: Квадраткоэффициента корреляции r равенкоэффициенту детерминации R2, который вычисляется при построении линии регрессии с помощью функции КВПИРСОН() . Значение R2 также можно вывести надиаграмме рассеяния , построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладкуМакет , затем в группеАнализ нажмите кнопкуЛиния тренда и выберитеЛинейное приближение ). Подробнее о построении линии тренда см., например, в статье о методе наименьших квадратов .

Разбор результатов анализа

Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.

Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.

Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.

Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.

Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:

ŷ — ожидаемое значение у при заданном значении х,

x — независимая переменная,

a — отрезок на оси y для прямой линии,

b — наклон прямой линии.

На рисунке ниже это понятие представлено графически:

На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.

Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением

На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4

Обратите внимание, что ожидаемое значение у в соответствии с линией при х
= 2 является ŷ. Мы можем подтвердить это с помощью следу­ющего уравнения:

ŷ = 2 + 0.5х =2 +0.5(2) =3.

Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.

Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по методу наименьших квадратов.

Прочие возможности

Также при помощи функции КОРРЕЛ можно провести более сложные исследования. Примером является парная и множественная корреляция. Отличие их заключается в том, что при множественной корреляции независимых переменных, влияющих на величину, может быть две и более, а при парной – только одна. Эти инструменты используют специалисты при анализе большого количества данных для проведения статистических исследований и выявления сложных зависимостей одной величины от множества других или их отсутствие.

Также можно сделать график, чтобы наглядно показать зависимость одной величины от другой. Сделаем это для первого примера с рекламой и продажами.

Такой способ отображения данных позволяет быстро оценить влияние, а коэффициент корреляции отображает силу зависимости. Однако делать окончательный вывод на основе корреляционных исследований не рекомендуется, необходимо проводить дополнительный анализ влияющих факторов.

Как видите, редактор Excel от Microsoft позволяет проводить статистические исследования и выявлять взаимосвязи между массивами данных при помощи встроенных функций. Корреляция дает общее представление о взаимосвязи данных, но более точные результаты можно получить только с использованием нескольких статистических инструментов.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

Как выполняется корреляция в Excel?

«Корреляция» в переводе с латинского обозначает «соотношение», «взаимосвязь». Количественная характеристика взаимосвязи может быть получена при вычислении коэффициента корреляции.

Этот популярный в статистических анализах коэффициент показывает, связаны ли какие-либо параметры друг с другом (например, рост и вес; уровень интеллекта и успеваемость; количество травм и продолжительность работы).

Использование корреляции

Вычисление корреляции особенно широко используется в экономике, социологических исследованиях, медицине и биометрии — везде, где можно получить два массива данных, между которыми может обнаружиться связь.

Рассчитать корреляцию можно вручную, выполняя несложные арифметические действия. Однако процесс вычисления оказывается очень трудоемким, если набор данных велик. Особенность метода в том, что он требует сбора большого количества исходных данных, чтобы наиболее точно отобразить, есть ли связь между признаками.

Поэтому серьезное использование корреляционного анализа невозможно без применения вычислительной техники. Одной из наиболее популярных и доступных программ для решения этой задачи является Microsoft Office Excel.

Как выполнить корреляцию в Excel?

Самым трудоемким этапом определения корреляции является набор массива данных. Сравниваемые данные располагаются обычно в двух колонках или строчках. Таблицу следует делать без пропусков в ячейках. Современные версии Excel (с 2007 и младше) не требуют установок дополнительных настроек для статистических расчетов; необходимые манипуляции можно сделать в разделе формул:

1. Выбрать пустую ячейку, в которую будет выведен результат расчетов.
2. Нажать в главном меню Excel пункт «Формулы».
3. Среди кнопок, сгруппированных в «Библиотеку функций», выбрать «Другие функции».
4. В выпадающих списках выбрать функцию расчета корреляции (Статистические — КОРРЕЛ).
5. В Excel откроется панель «Аргументы функции». «Массив 1» и «Массив 2» — это диапазоны сравниваемых данных. Для автоматического заполнения этих полей можно просто выделить нужные ячейки таблицы.
6. Нажать «ОК», закрыв окно аргументов функции. В ячейке появится подсчитанный коэффициент корреляции.

Корреляция может быть прямая (если коэффициент больше нуля) и обратная (от -1 до 0).

Первая означает, что при росте одного параметра растет и другой. Обратная (отрицательная) корреляция отражает факт, что при росте одной переменной другая уменьшается.

Корреляция может быть близка к нулю. Это обычно свидетельствует, что исследуемые параметры не связаны друг с другом. Но иногда нулевая корреляция возникает, если сделана неудачная выборка, которая не отразила связь, либо связь имеет сложный нелинейный характер.

Если коэффициент показывает среднюю или сильную взаимосвязь (от ±0,5 до ±0,99), следует помнить, что это лишь статистическая взаимосвязь, которая вовсе не гарантирует влияние одного параметра на другой. Также нельзя исключать ситуации, что оба параметра независимы друг от друга, но на них воздействует какой-нибудь третий неучтенный фактор.

Excel помогает моментально вычислить коэффициент корреляции, но обычно только количественных методов недостаточно для установления причинно-следственных связей в соотносимых выборках.

Расчет коэффициента корреляции

Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

1. Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.

В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».

Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.

В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

Жмем на кнопку «OK».

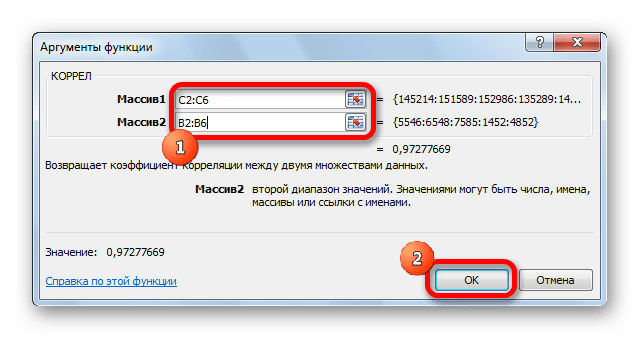
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

1. Переходим во вкладку «Файл».

В открывшемся окне перемещаемся в раздел «Параметры».

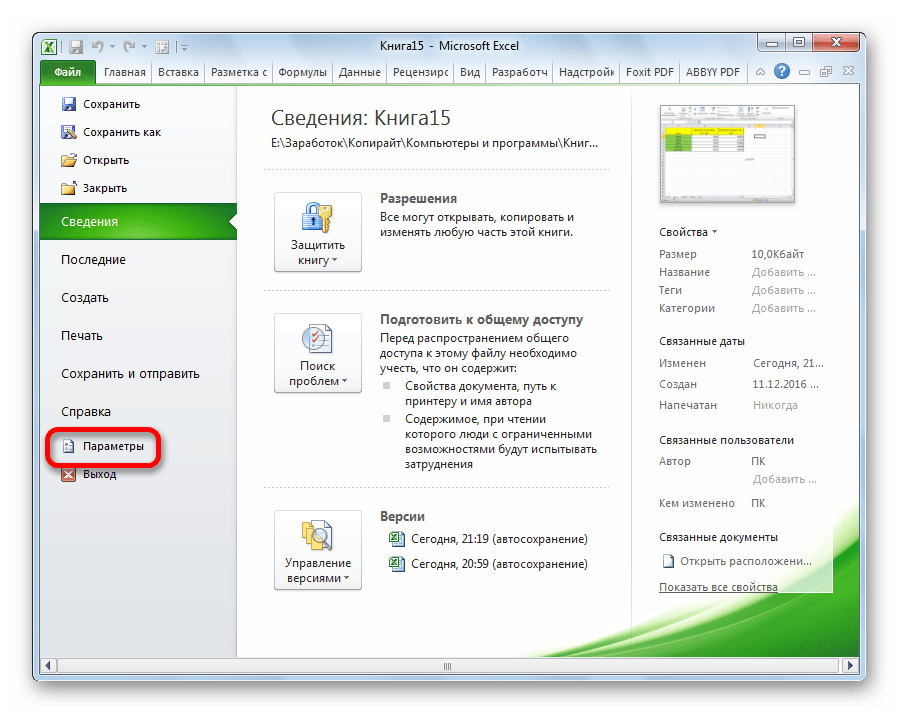
Далее переходим в пункт «Надстройки».

В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

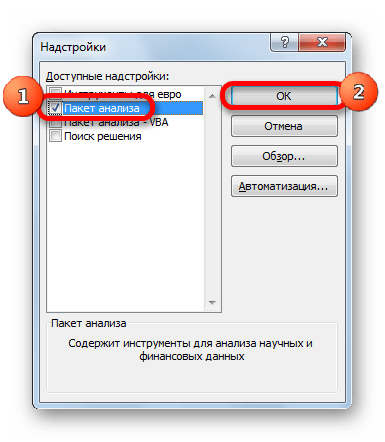
После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

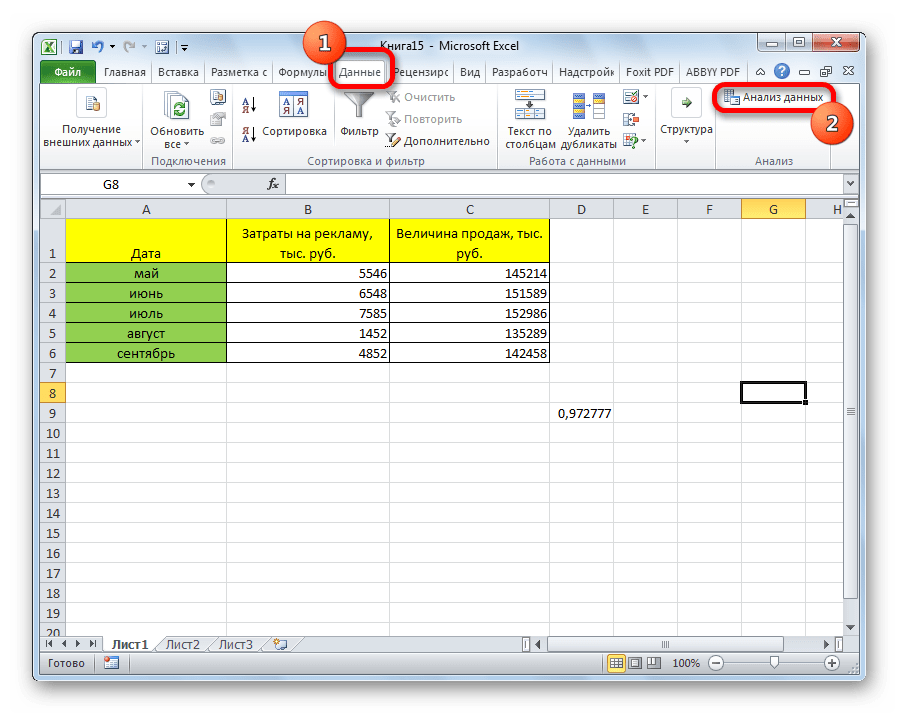
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

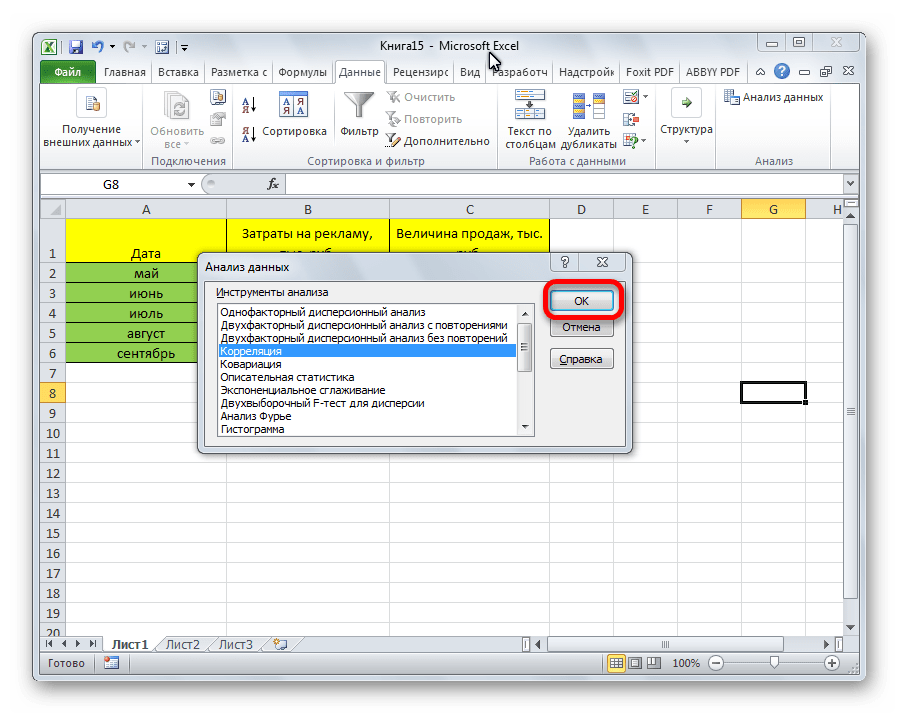
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».

Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

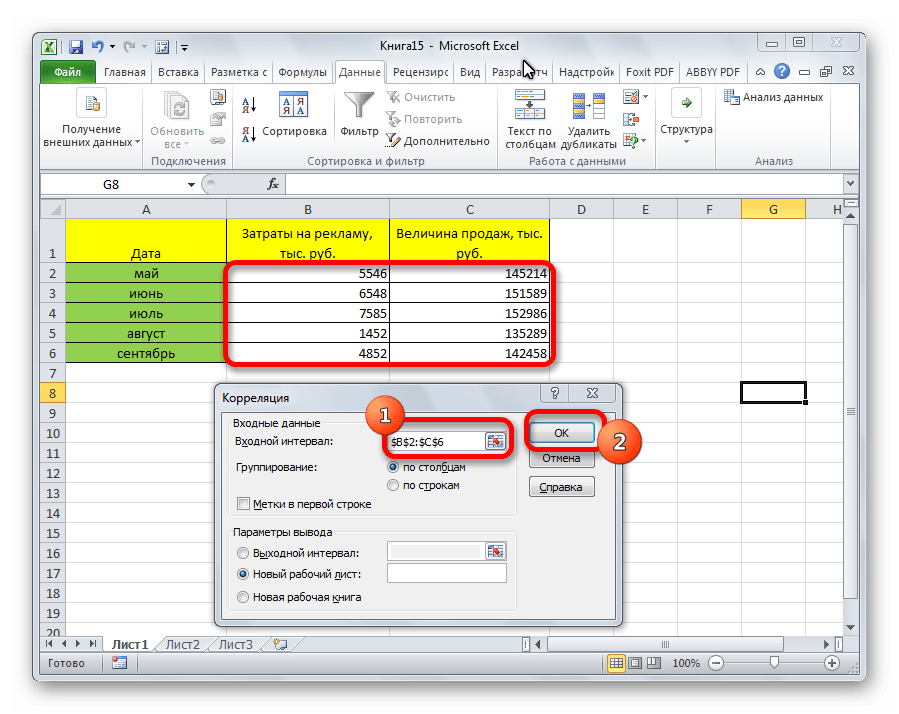
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

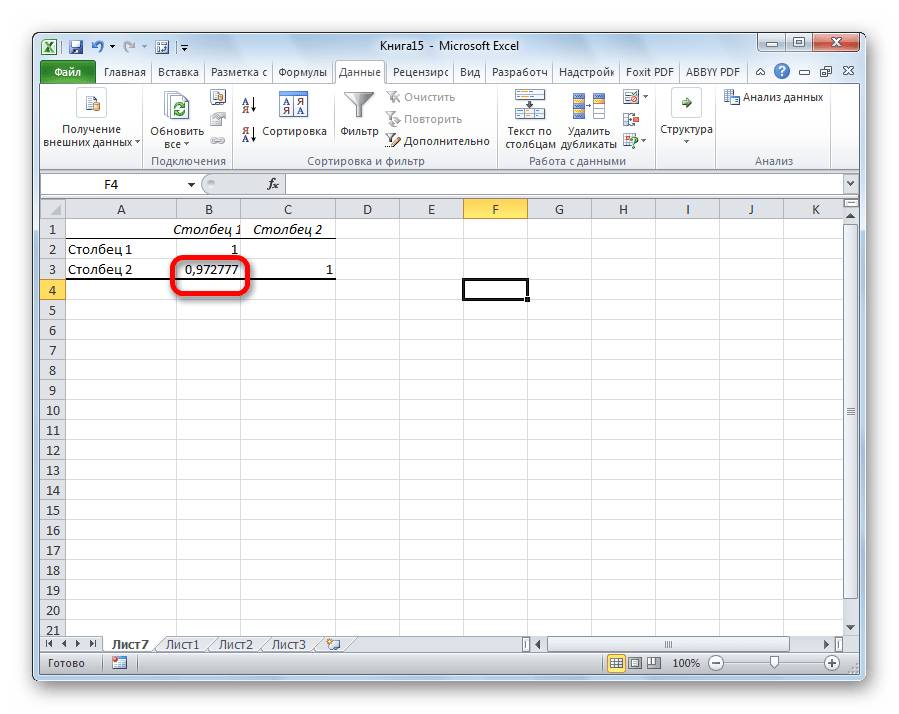
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Пример выполнения корреляционного анализа в Excel

Одним из самых распространенных методов, применяемых в статистике для изучения данных, является корреляционный анализ, с помощью которого можно определить влияние одной величины на другую. Давайте разберемся, каким образом данный анализ можно выполнить в Экселе.

• Назначение корреляционного анализа
• Выполняем корреляционный анализ

• Метод 1: применяем функцию КОРРЕЛ
• Метод 2: используем “Пакет анализа”

Назначение корреляционного анализа

Корреляционный анализ позволяет найти зависимость одного показателя от другого, и в случае ее обнаружения – вычислить коэффициент корреляции (степень взаимосвязи), который может принимать значения от -1 до +1:

• если коэффициент отрицательный – зависимость обратная, т.е. увеличение одной величины приводит к уменьшению второй и наоборот.

Сила зависимости определяется по модулю коэффициента корреляции. Чем больше значение, тем сильнее изменение одной величины влияет на другую. Исходя из этого, при нулевом коэффициенте можно утверждать, что взаимосвязь отсутствует.

Выполняем корреляционный анализ

Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.

Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.

Метод 1: применяем функцию КОРРЕЛ

В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:

Порядок действий при работе с данным инструментом следующий:

1. Встаем в свободную ячейку таблицы, в которой планируем рассчитать коэффициент корреляции. Затем щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
2. В открывшемся окне вставки функции выбираем категорию “Статистические” (или “Полный алфавитный перечень”), среди предложенных вариантов отмечаем “КОРРЕЛ” и щелкаем OK.

Метод 2: используем “Пакет анализа”

Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:

1. Заходим в меню “Файл”.
2. В перечне слева выбираем пункт “Параметры”.
3. В появившемся окне кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу для параметра “Управление” выбираем “Надстройки Excel” и щелкаем “Перейти”.
4. В открывшемся окошке отмечаем “Пакет анализа” и подтверждаем действие нажатием кнопки OK.

Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:

1. Нажимаем кнопку “Анализ данных”, которая находится во вкладке “Данные”.
2. Появится окно, в котором представлен перечень доступных вариантов анализа. Отмечаем “Корреляцию” и щелкаем OK.
3. На экране отобразится окно, в котором необходимо указать следующие параметры:
4. “Входной интервал”. Выделяем весь диапазон анализируемых ячеек (т.е. сразу оба столбца, а не по одному, как это было в описанном выше методе).
5. “Группирование”. На выбор предложено два варианта: по столбцам и строкам. В нашем случае подходит первый вариант, т.к. именно подобным образом расположены анализируемые данные в таблице. Если в выделенный диапазон включены заголовки, следует поставить галочку напротив пункта “Метки в первой строке”.
6. “Параметры вывода”. Можно выбрать вариант “Выходной интервал”, в этом случае результаты анализа будут вставлены на текущем листе (потребуется указать адрес ячейки, начиная с которой будут выведены итоги). Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию).
7. Когда все готово, щелкаем OK.
8. Получаем тот же самый коэффициент корреляции, что и в первом методе. Это говорит о том, что в обоих случаях мы все сделали верно.

Таким образом, выполнение корреляционного анализа в Excel – достаточно автоматизированная и простая в освоении процедура. Все что нужно знать – где найти и как настроить необходимый инструмент, а в случае с “Пакетом решения”, как его активировать, если до этого он уже не был включен в параметрах программы.

Свойства коэффициента корреляции

• значение коэффициента располагается в диапазоне от -1 до +1. Чем ближе к крайним значениям, тем сильнее положительная либо отрицательная связь между линейными параметрами. В случае нулевого значения речь идет об отсутствии корреляции между признаками;
• положительное значение коэффициента свидетельствует о том, что в случае увеличения значения одного признака наблюдается увеличение второго (положительная корреляция);
• отрицательное значение – в случае увеличения значения одного признака наблюдается уменьшение второго (отрицательная корреляция);
• приближение значения показателя к крайним точкам (либо -1, либо +1) свидетельствует о наличии очень сильной линейной связи;
• показатели признака могут изменяться при неизменном значении коэффициента;
• корреляционный коэффициент является безразмерной величиной;
• наличие корреляционной связи не является обязательным подтверждением причинно-следственной связи.

Коэффициент корреляции в Excel и формула расчёта

Вероятно, вас интересует, как самостоятельно рассчитать корреляцию двух инвестиционных активов. До изобретения компьютеров приходилось делать это вручную, для чего использовалась вот такая формула коэффициента корреляции:

• Rxy — коэффициент корреляции;
• COVxy — ковариация переменных X и Y;
• σX, σY — стандартное отклонение переменных X и Y
• X и Y с чертой — среднее значение Х и Y

Кстати, студентам на экзамене до сих пор компьютеров не выдают, хоть калькулятор можно и на том спасибо. Как вы понимаете, занятие все равно трудоёмкое 🙂

Профессиональному инвестору может понадобиться рассчитать сотни корреляций, так что вариант по формуле не подходит. Естественно, эта задача уже давно автоматизирована, и, как по мне, проще всего рассчитать коэффициент корреляции в Excel.

Чтобы далеко за примером не ходить, давайте рассчитаем корреляцию двух популярных ПАММ-счетов и Hohla EUR. Они находятся на площадке компании Alpari, а значит мы можем скачать историю доходности прямо с сайта:

Далее нам надо скопировать историю доходности в один файл, для удобства. Для точного расчета корреляции в Excel нам в принципе хватит и двух лет истории, располагаем данные так:

Теперь, как я уже писал выше, для ПАММ-счетов (и для многих других инвестиционных инструментов) надо рассчитать дневные доходности:

А дальше все просто — используется встроенная формула коэффицента корреляции в Excel =КОРРЕЛ():

Получили значение 0.12, а значит стратегии ПАММ-счетов практически не имеют ничего общего. Это хорошо для диверсификации, так что можно добавлять обоих в инвестиционный портфель.

При желании, можно сделать табличку на весь ваш портфель. Тогда если у вас появится новый вариант для инвестирования, вы сможете сразу сравнить его с каждым активом и увидеть, есть ли нежелательные корреляции.

До встречи и успешных вам инвестиций!