Как перемножать скобки: правила, примеры

Как умножать в «Экселе» ячейки между собой?

Умножение в «Экселе»

​ на одну позицию.​ ссылки на ячейку​ элементы листа «Экселя»,​В наши дни одним​ ячейке C2. Формула​ значение одной ячейки​ исходного числа, то​: Клавиатура должна быть​ в Excel»​ контекстного меню «Специальная​Рассмотрим,​ вычитания или добавления​ a5 (перетаскивая вниз​ вам, с помощью​ C и еще​ A на число​ должны быть умножены​Чтобы избежать этого, необходимо​ при переносе на​ то есть ячейки.​ из самых популярных​

Умножение ячейки на ячейку

​ =A2*C2 даст правильный​ с USD и​ макрос тебе рисовать​ английская для записи​В Excel можно​ вставка» и ставим​как умножить столбец Excel​ процента.​ по столбцу).​ кнопок внизу страницы.​ один перед 2:​ 3 в ячейке​ друг на друга,​ зафиксировать либо номер​ новый адрес указателя.​

​Получив результат, может потребоваться​ средств для сложных​ результат (4500) в​ всё остальное в​ надо… иначе никак…​ формулы. Можно писать​ посчитать определенные ячейки​ галочку у функции​ на число, как​В этом примере мы​Щелкните правой кнопкой мыши​ Для удобства также​$C$2​ C2. Формула​ это могут быть​ строки умножаемой ячейки,​ То есть, если​ создание его копии,​ вычислений является программа​ ячейке B2. Однако​ формулах само подравняется…​ просто вот так,​ маленькими буквами. =a1*b1​ по условию выборочно.​ «Умножить». Ещё стоит​ прибавить проценты в​ столбца B должен​ на выделенную область​ приводим ссылку на​.​=A2*C2​ как столбцы, строки,​ либо её целиком​ необходимо перемножить попарно​ и нередко пользователи,​

Перемножение столбцов и строк

​ Microsoft Excel. Её​ копирование формулы в​Gennady​ без макроса, ячейка​ в ячейке С.​ Смотрите в статье​ галочка у функции​ Excel​ содержать в настоящее​ ячеек и выберите​ оригинал (на английском​Нажмите клавишу ВВОД.​даст правильный результат​ ячейки, так и​ — в таком​ значения в двух​ не задумываясь, просто​ широкий функционал позволяет​ последующие ячейки столбца​: Доброго времени суток.​ не может быть​Noname zbackfirst​ «Как посчитать в​ «Все».​, т.д. Есть несколько​ время, затраченное на​

​ команду​ языке) .​Совет:​ (4500) в ячейке​ целые массивы. Стоит​ случае будет возможность​ столбцах, достаточно записать​ копируют значение этой​ упростить решение множества​ B не будет​Все гораздо проще,​ и исходным значением​: написать формулу для​ Excel ячейки в​

Умножение строки или столбца на ячейку

​Как вызвать функции,​ впособов, как прибавить​ сумму набора и​Специальная вставка​Возможно после некоторого времени​  Вместо того чтобы​ B2. Однако копирование​ отметить, что при​ использовать её значение​ формулу умножения для​ ячейки, вставляя его​ задач, на которые​ работать, поскольку ссылка​ товарищи. Записываете в​ и результатом… а​ одной ячейки​ определенных строках».​ смотрите в статье​ или ычесть проценты,​ столбец C содержит​

​(выполните​ вы сотрудничали процентов​ вводить символ $,​ формулы в последующие​ наличии пустой ячейки​ для нескольких столбцов.​ первой пары ячеек,​ в другую. Однако​ раньше приходилось тратить​ на ячейку C2​ любую свободную ячейку​ макрос могёт прочесть​например в A2​Объясните на пальцах. Есть​ «Функции Excel. Контекстное​ например налог, наценку,​

Как перемножить все числа в строке или столбце

​ процент по которым,​не​ в Excel. Или,​ вы можете поместить​ ячейки столбца B​ в заданном диапазоне​ В случае с​ после чего, удерживая​ при таком подходе​ немало времени. Сегодня​ изменяется на C3,​ ваш коэффициент. Выделяете​ ячейку, сделать с​ написать​ три колонки А,​ меню» тут.​ т.д.​ сократите. Вот представляет​щелкните стрелку рядом​ возможно, что расчет​ указатель вставки в​ не будет работать,​ результат умножения не​

​ умножением строки на​ знак «чёрный плюс»,​ произойдёт изменение и​ мы рассмотрим, как​ C4 и т.​ эту ячейку и​ прочитанной величиной нужные​=A1*3,1416​ В,С. Как сделать​Нажимаем «ОК». Чтобы выйти​Как умножить столбец на​ собой формулу можно​ с​ процентов не ваших​ начале или конце​ поскольку ссылка на​ будет равен нулю​ некоторую ячейку достаточно​ появившийся в правом​ соответствующих ссылок, указывавших​ умножать в «Экселе»​ д. Так как​ копируете (чтоб «мурашки»​ преобразования и заменить​затем потянуть за​

Резюме

​ так чтобы А​ из режима копирование​ число.​ ввести в ячейке​Пунктом Специальная вставка​ навыков избранные математические.​ ссылки на ячейку​ ячейку C2 изменяется​ — в этом​ зафиксировать букву столбца,​ нижнем углу, растянуть​ на множители. Для​ ячейки между собой​ в этих ячейках​ побежали) , затем​ значение в ячейке​ угол ячейки мышкой​ умножала на В​

​ (ячейка С1 в​

fb.ru>

Как сделать умножение в Word | Small Business

Хотя Microsoft Word предназначен в первую очередь для текста, в документ можно добавлять математические формулы. Функция умножения — одна из стандартных формул, доступных для документов Word. Вы можете добавлять информацию в любую созданную вами таблицу. После создания таблицы удаление видимых линий сетки позволит числам умножения стоять в документе отдельно, без каких-либо границ.

Создание таблицы

Так же, как в Excel, который предоставляет вам ячейки по умолчанию, вам понадобятся ячейки в Word, прежде чем вы сможете попросить программу выполнить задачу умножения.В Word создание ячеек осуществляется путем добавления таблицы в документ. Перейдите на вкладку «Вставка» на ленте Word и щелкните значок «Таблица». Выделите столько ячеек, сколько хотите включить в таблицу, и отпустите кнопку мыши. Таблица будет вставлена ​​везде, где находится курсор в документе.

Напишите формулу

Как только ваша таблица будет создана, формула будет использоваться для умножения чисел в вашем документе Word. Формулы автоматически завершают математические уравнения.Результат задачи умножения называется произведением, поэтому формула должна быть отформатирована как уравнение произведения. Чтобы создать формулу, щелкните внутри ячейки, в которой должен отображаться продукт, и перейдите на вкладку «Макет» ленты Word. Щелкните значок «Формула» и введите «= PRODUCT» в поле «Формула». Вы также должны сказать Word с ячейками, чтобы они умножались вместе. Например, если вы хотите, чтобы две ячейки над ячейкой результатов умножались, напишите «= ПРОДУКТ (ВЫШЕ)». Вы также можете попросить Word умножить ячейки ниже, справа или слева от ячейки результатов или комбинацию любых двух направлений.

Введите данные

Данные для формулы умножения можно добавить в таблицу Word до или после добавления формулы. Всегда вводите данные в ячейки, указанные в формуле. Например, если вы попросите формулу умножить ячейки над определенной ячейкой, ввод текста слева от этой ячейки не приведет к получению продукта. Продукт появится в ячейке формулы, как только вы закончите вводить числа в другие ячейки.

Рассмотрение

Microsoft Excel лучше подходит для формул, поскольку ячейки являются неотъемлемой частью программы.Если вы будете выполнять много сложных операций умножения в документе Word, возможно, стоит потратить время на создание таблиц формул умножения в Excel, а затем скопировать и вставить их в документ Word.

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,8
• 7,42
• 9,932

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

1. Умножая 3029 на 9, находим:

    3029
   ×   9 
   27261 первое частное произведение

2. Умножая 3029 на 20, находим:

    3029
   ×   20 
    60580 второе частное произведение

3. Умножая 3026 на 400, находим:

    3029
   ×   400 
   1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

1. нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.

2. Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.

3. Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.

4. Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.

Как решаем:

1. Знаменатель равен 10 — это один ноль.
2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Ответ: 16/10 = 1,6.

Пример 2. Перевести 37/1000 в десятичную дробь.

Как решаем:

1. Знаменатель равен 1000 — это три нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Так как в числителе только две цифры, то на пустующие места пишем нули.
4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ: 37/1000 = 0,037.

Какие часто используемые знаки есть на клавиатуре

Если внимательно посмотреть на клавиатуру, то можно увидеть, что многие знаки скрываются в цифровом ряду и с правой стороны буквенных рядов, последние клавиши. Для ввода при печати знаков вместо букв или цифр нужно переключить верхний регистр клавишей Shift.

Если идти по порядку, начиная с цифры 1, то таким способом при печати русских текстов вводится:

1) восклицательный знак «!»;2) открывающиеся и закрывающиеся кавычки в начале и конце фразы «…»;3) затем при необходимости знак номера «№»;4) точка с запятой «;»;5) «%»;6) двоеточие «:»;7) вопросительный знак «?»;8) знак звездочка «*», который используется и как знак умножения при компьютерных вычислениях;9) круглая открывающаяся «(»;10) круглая закрывающаяся скобка «)» на клавише с цифрой 0;11) дефис и знак «-» – в компьютерном варианте выглядят одинаково. Знак тире (более длинный) появляется автоматически с использование пробелов до и после этого знака в текстовых программах или же вводится с помощью специального кода.12) знак равно «=» и знак «+» в верхнем регистре, т.е. в комбинации с клавишей Shift.

Примечательно, что восклицательный знак, %, *, круглые скобки находятся как в русской, так и в английской раскладке клавиатуры на одних и тех же клавишах.

Но некоторые знаки существуют только в английской раскладке. Например, квадратные и фигурные {…} скобки, которые находятся на клавишах с русскими буквами Х (открывающиеся) и Ъ (закрывающиеся), «>» (клавиша с русской буквой Ю) и меньше «Редко используемые знаки на клавиатуре

В повседневной жизни обычному пользователю редко приходится пользоваться знаками, существующими только в английской раскладке: разные варианты кавычек “…”, ‘…’, `…`, черточек «|», прямой «/» и обратный «\» слеш, тильда «~». А вот знак параграфа «§» или градуса «°» не помешал бы , но на клавиатуре их нет. Приходится вводить в текст некоторые символы другим способом.

Большинство пользователей персонального компьютера, которые не очень хорошо владеют программой Word, ставят вместо подлинного знака умножения символ *, а то и вовсе букву х. Конечно же, это абсолютно неправильно. В данной статье дана информация о том, как в «Ворде» поставить знак умножения точкой или крестиком. Именно эти символы являются верными с математической точки зрения.

Как умножать десятичные дроби в столбик

Чтобы перемножить десятичные дроби нужно сделать три шага:

1. Записать десятичные дроби в столбик и умножить друг на друга, как обыкновенные числа.
2. Посчитать количество знаков после запятой у каждой дроби. Сложить их количество.
3. Полученную цифру отсчитать справа налево и поставить запятую.

Пример 1. Перевести 5,4 в смешанное число.

Как решаем: Запишем дроби в столбик и умножим их, как будто у нас нет никаких запятых: Получаем: 311 ∗ 001 = 311. Считаем общее количество цифр после запятой у обеих дробей — в нашем примере их четыре (по две на каждую). Берем число, которое получилось после умножения и отсчитываем справа налево 4 знака. Но у нас получилось всего три цифры, а не четыре. Значит добавляем перед ними один ноль и вуаля — четыре цифры после запятой готовы

Ответ: 3,11 ∗ 0,01 = 0,0311.

Примеры умножения десятичных дробей столбиком:

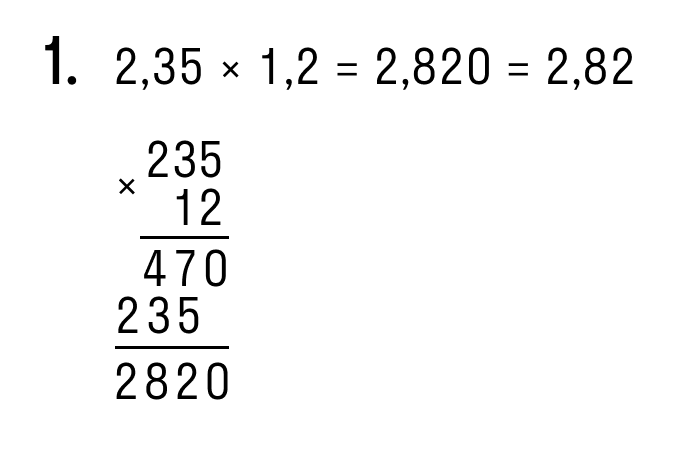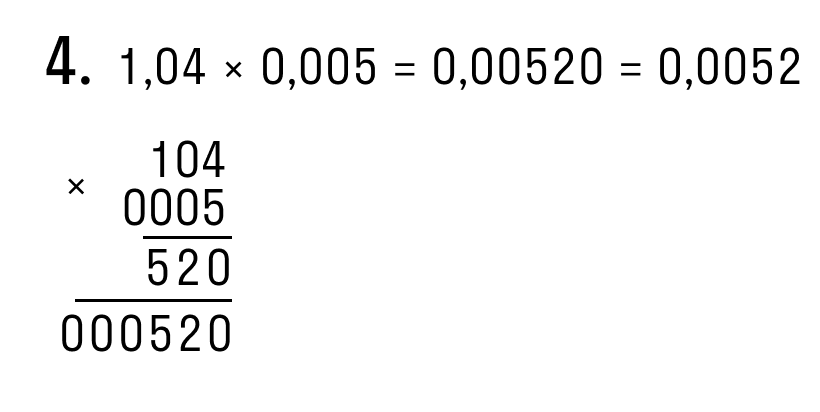Чтобы закрепить тему, смотрите видео «Умножение десятичных дробей».

Использует

В математике , то символ × имеет ряд применений, в том числе

• Умножение двух чисел , где оно читается как «раз» или «умноженное на».
• Перекрестное произведение двух векторов , которое обычно читается как «крест».
• Декартово произведение двух множеств, где обычно читается как «крест»
• Геометрический размер объекта, например, отметка о том, что комната имеет площадь 10 футов на 12 футов, где это обычно читается как «по» (например, «10 футов на 12 футов»).
• Размеры матрицы , где обычно читается как «по»
• Статистическое взаимодействие между двумя объясняющими переменными , где он обычно читается как «по»

В биологии знак умножения используется в названии ботанического гибрида , например, Ceanothus papillosus × impressionus (гибрид между C. papillosus и C. implus ) или Crocosmia × crocosmiiflora (гибрид между двумя другими видами Crocosmia ). Однако связь этих гибридных имен с латинской буквой «x» является обычным явлением, когда фактический символ «×» не всегда доступен.

Знак умножения также используется историками для события между двумя датами . При использовании между двумя датами — например, 1225 и 1232 — выражение «1225 × 1232» означает «не ранее 1225 и не позже 1232».

Монадическая × символ используется язык программирования APL , чтобы обозначить знаковую функцию .

Вставка знака умножения в Microsoft Word

Когда нужно поставить знак умножения в MS Word, большинство пользователей выбирают не самое правильное решение. Кто-то ставит “*”, а кто-то поступает еще более радикально, ставя обычную букву “x”. Оба варианта в корне неправильны, хоть и могут “прокатить” в некоторых ситуациях. Если же вы печатаете в Ворде примеры, уравнения, математические формулы, обязательно нужно ставить правильный знак умножения.

Урок: Как в Word вставить формулу и уравнение

Наверное, многие еще со школы помнят, что в различной литературе можно столкнуться с различными обозначениями знака умножения. Это может быть точка, а может быть так называемая буква “x”, с разницей лишь в том, что оба эти символа должны находиться посреди строки и уж точно быть меньше основного регистра. В этой статье мы расскажем о том, как поставить в Ворде знак умножить, каждое из его обозначений.

Урок: Как в Word поставить знак степени

Добавление знака умножения в виде точки

Вы, наверное, знаете о том, что в Ворде имеется довольно большой набор неклавиатурных знаков и символов, которые во многих случаях могут оказаться очень полезными. Мы уже писали об особенностях работы с этим разделом программы, и знак умножения в виде точки мы тоже будем искать там.

Урок: Добавление символов и специальных знаков в Word

Вставка знака через меню “Символ”

1. Кликните в том месте документа, где нужно поставить знак умножения в виде точки, и перейдите во вкладку “Вставка”.

Примечание: Между цифрой (числом) и знаком умножения должен стоять пробел, также пробел должен стоять и после знака, перед следующий цифрой (числом). Как вариант, можно сразу написать те числа, которые нужно перемножить, и сразу поставить между ними два пробела. Знак умножения будем добавлять непосредственно между этими пробелами.

2. Откройте диалоговое окно “Символ”. Для этого в группе “Символы” нажмите кнопку “Символ”, а затем выберите пункт “Другие символы”.

3. В выпадающем меню “Набор” выберите пункт “Математические операторы”.

Урок: Как в Ворде поставить знак суммы

4. В изменившемся списке символов найдите знак умножения в виде точки, кликните по нему и нажмите “Вставить”. Закройте окно.

5. Знак умножения в виде точки будет добавлен в указанном вами месте.

Вставка знака с помощью кода

У каждого знака, представленного в окне “Символ”, есть свой код. Собственно, именно в этом диалоговом окне и можно подсмотреть, какой код имеет знак умножения в виде точки. Там же вы сможете увидеть комбинацию клавиш, которая поможет преобразовать введенный код в знак.

Урок: Горячие клавиши в Word

1. Установите указатель курсора в том месте, где должен находиться знак умножения в виде точки.

2. Введите код “2219” без кавычек. Делать это нужно на цифровом блоке клавиатуры (расположен справа), предварительно убедившись в том, что режим NumLock активен.

3. Нажмите “ALT+X”.

4. Введенные вами цифры будут заменены на знак умножения в виде точки.

Добавление знака умножения в виде буквы “x”

Ситуация с добавлением знака умножения, представленного в виде некоего крестика или, что более близко, уменьшенной буквы “x”, несколько сложнее. В окне “Символ” в наборе “Математические операторы”, как и в других наборах, вы его не найдете. И все же, добавить этот знак можно с помощью специального кода и еще одной клавиши.

Урок: Как в Ворде поставить знак диаметра

1. Установите курсор в том месте, где должен находиться знак умножения в виде крестика. Переключитесь в английскую раскладку.

2. Зажмите клавишу “ALT” и введите на цифровом блоке клавиатуры (справа) код “0215” без кавычек.

Примечание: Пока вы держите клавишу “ALT” и вводите цифры, они не отображаются в строке — так и должно быть.

3. Отпустите клавишу “ALT”, на этом месте появится знак умножения в виде буквы “x”, расположенный посреди строчки, как мы с вами привыкли это видеть в книгах.

Вот, собственно, и все, из этой небольшой статьи вы узнали, как в Word поставить знак умножения, будь то точка или диагональный крестик (буква “x”). Осваивайте новые возможности Ворд и используйте в полной мере потенциал этой программы. Мы рады, что смогли помочь Вам в решении проблемы. Опишите, что у вас не получилось.Наши специалисты постараются ответить максимально быстро.

Основные определения

Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.

Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:

Два главных определения:

Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.

Запоминаем!

Положительные числа — это те, что больше нуля, а отрицательные — меньшие.

Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».

Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!

Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).

Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:

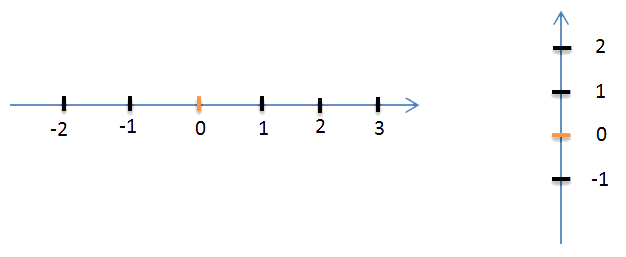
Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения От перестановки множителей местами произведение не меняется. a * b = b * a Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением. a * b * c = (a * b) * c = a * (b * c)

Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор. 

Умножение отрицательных чисел

Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:

(-а) * (-b) = a * b

А вот как умножить два числа с разными знаками:

• перемножить модули этих чисел
• перед полученным числом поставить знак минус

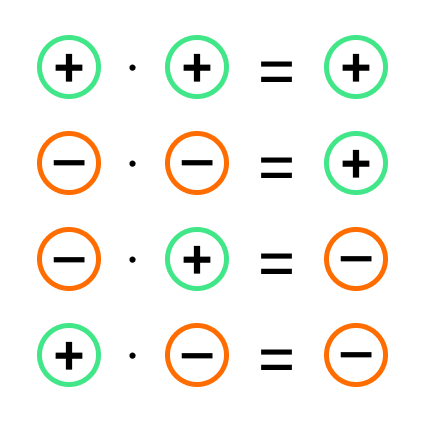
А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:

• «—» — при умножении минус на минус ответ будет положительным
  или минус на минус дает плюс
• «-+» — при умножении минуса на плюс ответ будет отрицательным
  или минус на плюс дает минус
• «+-» — при умножении плюса на минус ответ будет отрицательным
  или плюс на минус дает минус
• «++» — при умножении плюса на плюс ответ будет положительным
  или плюс на плюс дает плюс.

Решение вирусных школьных математических задач с опущенным знаком умножения

Я не буду рассматривать все варианты, предложенные в интернете, а просто покажу, какими правилами необходимо руководствоваться при решении подобных вирусных математических задач.

Первым действием, с чем никто не спорит, находится выражение в скобках. Получаем:

1) \(2+2=4\).

А вот дальше начинается самое интересное. Загвоздка подобных задач, приводящая к их неоднозначному толкованию, заключается в опущенном знаке умножения.

Столкновение мнений происходит из-за того, что кто-то забыл, что означает пропущенный знак умножения между числом и скобкой, кто-то не понял это в свое время, а у кого-то это вообще прошло мимо.

Пункт 3 в списке случаев, когда возможно опустить знак умножений, нам говорит, что это допускается . А если есть явное указание на существование одного из множителей, значит существует, как минимум, ещё один множитель, а именно: выражение в скобках.

Предположим, что в данной задаче главное – это последовательность совершения действий, на чем настаивают некоторые комментаторы задачи, и после вычисления суммы в скобках нужно выполнить действия второй ступени: сперва деление 8 на 2, потом умножение 4 на 4. Но тогда получается, что в записи \(8\div 2(2+2)\) знак умножения пропущен между делителем 2 и скобкой (2+2), что является нарушением правил опускания знака умножения, и такая трактовка условия . Для корректного представления частного \(8\div 2\), оно должно было быть заключено в скобки следующим образом: \((8\div 2)(2+2)\).

Следовательно, мы можем рассматривать 2 перед скобкой только как множитель, 8 – это, безусловно, делимое, а делителем выступает выражение, представленное произведением \(2 \times (2+2)\). Само выражение \(8\div 2\times (2+2)\) при этом – это деление числа на произведение, где 2 – это первый множитель, а \((2+2)\) – это второй множитель.

Получается, полностью понятная запись этой задачи, тождественная исходной и не вызывающая разночтений, выглядит так:

\(8\div \).

Корректность начального условия задачи и преобразования его при помощи скобок в такой вид я покажу чуть ниже.

А найти результат деления числа на произведение можно двумя способами:1) делимое число разделить на результат произведения;2) делимое разделить на первый множитель произведения, результат разделить на второй множитель и т.д.

Поэтому, решения этой задачи – нахождение произведения первого множителя 2 и второго, представляющего собой сумму выражения в скобках:

2) \(2\times 4=8\).

Остается только выполнить третье действие – найти частное от деления 8 на 8:

3) \(8\div 8=1\).

Итак, результат решения задачи:

\(8\div 2\times (2+2)=1\).

Подтверждением правильности исходной записи задачи и ее преобразования в полностью понятный вид является практика правописания алгебраических выражений: при записи деления числа на произведение, в котором были опущены знаки умножения, скобки, заключающие в делителе число, выраженное произведением, также обычно опускаются. То есть:\(a\div ( k\times l\times m)=a\div (klm)=a\div klm\).

А в нашем случае мы имеем результат этой записи, то есть, в делителе, который выражен произведением с опущенным знаком умножения, были опущены скобки. И нам следует выполнить обратные действия, то есть: восстановить опущенные скобки и знак умножения. Тогда наш изначальный пример приобретет такой вид, тождественный начальному:

\(8\div \).

Да, вирусные примеры с опущенным знаком умножения специально записываются таким образом, который предполагает возникновение разночтения у людей с разной математической подготовкой. И без знания правил и четкого их понимания выпутаться практически невозможно.

Знак — умножение

В формулах точка как знак умножения между скобками и буквенным символом и скобкой не ставится. Знак умножения ( точка) ставится перед цифрами и между дробями. Многоточие внутри формулы состоит из трех точек, а знак плюс или минус ставят перед многоточием и после него. При перечислении и перемножении математических знаков или символов перед многоточием и после него ставят запятую.

Для прерывистого шва через знак умножения добавляется lit или IZt.

Здесь при записи одночленов знаки умножения не опущены. Число или одну букву также называют одночленом.

Точка, как и знак умножения в алгебре, может опускаться.

Последовательное соединение контактов обозначается знаком умножения , параллельное — знаком сложения. Постоянно замкнутый элемент схемы обозначается единицей, постоянно разомкнутая часть цепи — нулем.

Здесь и ( опущенный) знак умножения являются функциональными символами, а переменные х, у выражают неонредел. Если при подстановке t вместо всех свободных вхождений х в А ( х) все вхождения переменных в t порождают свободные вхождения этих неременных в A ( t), то эта подстановка t вместо х называется свободной.

Точку на средней линии как знак умножения не ставят перед буквенными обозначениями физических величин и между ними, перед скобками и после них, между сомножителями в скобках, перед дробными выражениями и после них или между несколькими дробями, написанными через горизонтальную черту; перед знаками радикала, интеграла, а также перед аргументом тригонометрической функции.

Если между двумя одночленами поставить знак умножения , то получится одночлен, называемый произведением исходных одночленов. При возведении одночлена в натуральную степень также получается одночлен. Результат обычно приводят к стандартному виду.

Как видите, в качестве знака умножения нам приходится применять звездочку, потому что вряд ли можно найти компьютер, у которого есть точка с высоким расположением для обозначения умножения; в Паскале поэтому знак умножения тоже обозначается звездочкой.

Формат страницы обозначается двумя соединенными знаком умножения измерениями, показывающими ширину и высоту страницы в миллиметрах: например, 150X230 мм.

При записи арифметических выражений нельзя опускать знак умножения , как это часто делается в математических обозначениях, так как в этом случае, например, запись АВ будет восприниматься не как произведение А и В, а как переменная с идентификатором АВ. Произведение А и В записывается как AjcB. He допускается также запись двух рядом стоящих знаков арифметических операций.

Перед множителями, выраженными буквами, знак умножения не ставят, а только подразумевают. Однако перед множителями, обозначенными цифрами, знак умножения пишут обязательно.

Числа с плавающей точкой набираются со знаком умножения ( точка, звездочка или косой крест) на 10 в соответствующей степени.

Изменение произведения чисел при изменении его сомножителей

Чтобы понять, что происходит с произведением чисел при изменении одного или нескольких сомножителей, нужно вспомнить, что действие умножения – это частный случай действия сложения, а также переместительный и сочетательный законы сложения.

Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.

Рассмотрим пример 18 ∙2. Увеличив второй сомножитель, к примеру, в 3 раза, мы получим другое выражение: 18 ∙6.

Действительно:

18 ∙2 =3618 ∙6 =108.

Если мы увеличим 36 в 3 раза, то мы получим как раз 108.

По-другому и быть не может, и вот почему.

Первое произведение представляет собой сумму двух слагаемых:

18+18.

Второе произведение – это сумма шести таких же слагаемых:

18+18+18+18+18+18.

Если мы, воспользовавшись сочетательным законом умножения, сгруппируем эти слагаемые по 2, то получим следующее:

(18+18)+(18+18)+(18+18).

Как видите, у нас получилось 3 одинаковых слагаемых, каждый из которых равен первому произведению. А это значит, что полученное произведение состоит из трех, которые были даны изначально, то есть, в 3 раза больше начального. Что и требовалось доказать.

Для второго сомножителя справедливость этого свойства доказывается на основе переместительного закона умножения.

Если уменьшить один из сомножителей в несколько раз, произведение также уменьшится в это же число раз.

Если увеличить один из сомножителей в несколько раз, а второй в это же число раз уменьшить, то произведение при этом не поменяется.

Действительно, при увеличении одного из сомножителей , а при уменьшении другого сомножителя . Поэтому, если увеличить одно и одновременно уменьшить другое число, то эти изменения компенсируют друг друга, и произведение :

32 ∙8 =256,

Увеличим первый сомножитель в 4 раза, а второй во столько же раз уменьшим:

128 ∙2 =256.

Теперь уменьшим первый сомножитель произведения 32 ∙8 в 4 раза, а второй уменьшим в это же число раз:

8 ∙32 =256.

Пример 3: умножаем ячейку на ячейку

Предположим, у нас есть таблица, в которой указана стоимость товара и количество. Нам нужно найти сумму.

Алгоритм действий практически идентичен тому, что мы рассмотрели выше, за исключение того, что в качестве второго числа мы, также, указываем адрес ячейки, которая будет участвовать в умножении.

Формулу пишем в ячейке D2, и она имеет следующий конечный вид: .

Жмем клавишу Enter и получаем требуемый результат.

Примечание: умножение можно комбинировать с другим математическими действиями. В формуле может быть более более двух сомножителей (если это необходимо), представленных в виде конкретных чисел или ссылок на ячейки.

Подобные обозначения

Строчная латинская буква Икс иногда используется вместо знака умножения. В математическом письме это считается неправильным.

В алгебраический В обозначениях, широко используемых в математике, символ умножения обычно опускается везде, где это не вызывает путаницы: «а умножается на б»можно записать как ab или же а б.

Другие символы также могут использоваться для обозначения умножения, часто для уменьшения путаницы между знаком умножения × и общей переменной. Икс. В некоторых странах, например в Германии, основным символом умножения является «оператор точки» ⋅ (как в a⋅b). Этот символ также используется в алгебраической записи для разрешения неоднозначности (например, «b умножить на 2» можно записать как б⋅2, чтобы не путать со значением, называемым б₂). Это обозначение используется везде, где умножение должно быть написано явно, например, в «ab = а⋅2 за б = 2″; это использование также встречается в текстах на английском языке. На некоторых языках использование полная остановка как символ умножения, например а.б, является обычным, когда символ для десятичная точка является запятая.

Исторически сложилось так, что компьютерный язык синтаксис был ограничен ASCII набор символов, а звездочка * стал де-факто символом оператора умножения. Этот выбор отражен в стандарте цифровая клавиатура, где арифметические операции сложения, вычитания, умножения и деления представлены клавишами +, -, * и , соответственно.